在很多学科中的很多计算任务中都需要用到曲线的曲率（或者曲率半径），numpy库里和matlab build-in里都没有现成的能从离散点来算曲率的方法，网上找到的代码又不敢直接用，毕竟是要高频率用到自己科研上的工具，所以决定结合找到的资料自己推一下，并造出python和matlab的轮子，造福后人

公式很简单：

曲率：

\kappa = \frac{|\ddot{\vec{r}}\times\dot{\vec{r}}|}{\left| \dot{\vec{r}}\right|^3}

在二维情况下，其标量形式为：

\kappa = \frac{|x''y'-x'y''|}{\left( (x')^2+(y')^2\right)^{3/2}}

所以对于解析情况非常简单，可以直接对于曲线表达式进行解析求导，但是对于离散的点，情况反倒会比较复杂，因为这里的x和y的一阶和二阶导数如果直接用差分方法来计算的话会造成比较大的误差。

这里比较保险的做法是，使用三个点确定的二次曲线的的曲率作为我们估计的曲率:

然后使用中间这个点(x2,y2)处的曲率作为这三个点的曲率估计

具体方法是先表示成参数方程的样子，

对于曲线参数t，有：

\left\{ \begin{matrix} x = a_1 +a_2 t+a_3 t^2\\ y= b_1 +b_2 t+b_3 t^2 \end{matrix} \right.

6个未知数，三个点里有6个已知分量，列六个方程，解出这 (a1,a2,a3), (b1,b2,b3)即可。

这里使用两段矢量的长度来作为取值范围：

t_a = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}\\ t_b = \sqrt{(x_3-x_2)^2 + (y_3-y_2)^2}

这里我们希望参数方程中的t满足如下条件：

(x,y)|_{t=-t_a} = (x_1,y_1)\\ (x,y)|_{t=0} = (x_2,y_2)\\ (x,y)|_{t=t_b} = (x_3,y_3)

则有：

\left\{ \begin{matrix} x_1 &= & a_1 &- a_2 t_a +a_3 t_a^2\\ x_2 &= &a_1 &\\ x_3 &= &a_1 &+ a_2 t_b + a_3 t_b^2 \end{matrix} \right.

以及

\left\{ \begin{matrix} y_1 &= & b_1 &- b_2 t_a + b_3 t_a^2\\ y_2 &= &b_1 &\\ y_3 &= &b_1 &+ b_2 t_b + b_3 t_b^2 \end{matrix} \right.

写成矩阵形式：

\left( \begin{matrix} x_1\\ x_2\\ x_3\\ \end{matrix} \right) = \left( \begin{matrix} 1& -t_a &t_a^2\\ 1& 0 & 0\\ 1& t_b& t_b^2\\ \end{matrix} \right) \left( \begin{matrix} a_1\\ a_2\\ a_3\\ \end{matrix} \right)

以及

\left( \begin{matrix} y_1\\ y_2\\ y_3\\ \end{matrix} \right) = \left( \begin{matrix} 1& -t_a &t_a^2\\ 1& 0 & 0\\ 1& t_b& t_b^2\\ \end{matrix} \right) \left( \begin{matrix} b_1\\ b_2\\ b_3\\ \end{matrix} \right)

简写为：

X=M A\\ Y=M B

可以使用求矩阵逆的方式求解线性方程:

A = M^{-1}X\\ B = M^{-1}Y

有了(a1,a2,a3)和(b1,b2,b3)就有了曲线的解析方程，接下来就和解析求曲率一样了，先算变量导数：

x'= \left.\frac{dx}{dt}\right|_{t=0} = a_2\\ x''= \left.\frac{d^2x}{dt^2}\right|_{t=0} =2 a_3\\ y'= \left.\frac{dy}{dt}\right|_{t=0} = b_2\\ y''= \left.\frac{d^2y}{dt^2}\right|_{t=0} =2 b_3

然后就是最终的曲率：

\kappa = \frac{x''y'-x'y''}{\left( (x')^2+(y')^2\right)^{3/2}} = \frac{2(a_3 b_2-a_2 b_3)}{(a_2^2+b_2^2)^{3/2}}

这样，任意给定三个点，都可以估计出这三个点是比较【弯的】还是比较【直的】，直的曲率小，van的曲率大。

随手生成两个例子算算：

（1）圆形：

好理解，圆形所有地方都是一样弯

（2）正弦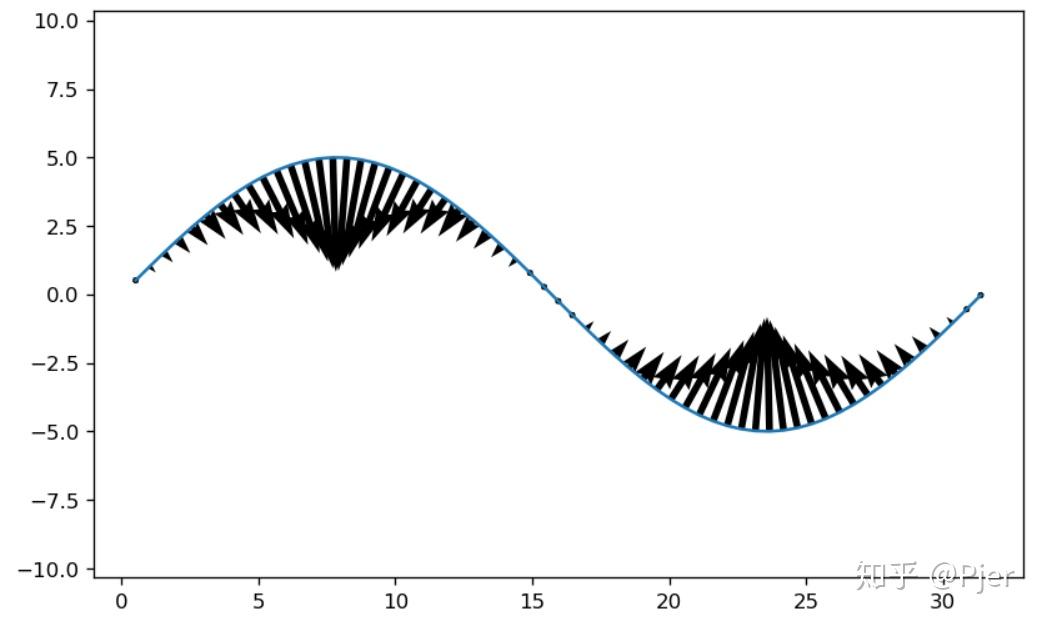

波峰和波谷最弯，0点附近最直。

看起来没毛病，核对了方向和曲率半径大小的数值，都能对上。这是一个可以放心使用的轮子

这里我把这个算法实现为Python和MATLAB，详见github：

引用方式：

[Cite] Pjer-zhang/PJCurvature

===================

Pjer内容分类整理：

精选 射电 编程 科研工具 太阳物理